I have been thinking of ways to incorporate maths into fun Christmas time activities recently and this one went down well with my 11 and 9 year old. This a great for a winter project and a way for kids to practise two skills:
- They will learn to recognize and describe symmetries of designs by finding centres of rotation and axis of symmetry.
- They will learn to make their own design with one or more specified symmetries.
Read on if you want to know how we made our snowflake and how I used it to teach my girls some maths...
You will need:
- Isometric paper - I used isometric paper with the girls to make it easier for them.
- A sharp pencil
- A ruler
STEP ONE
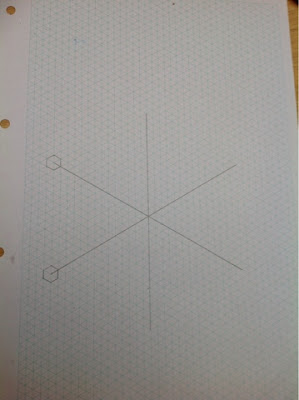
Draw a line down the centre of the page. We measured it out to be an even number. 12-16cm is best.
STEP TWO
Draw the two lines through the centre. To do this you will have to find the centre of the first line so you know where the other two lines should go through.
This is where the isometric paper helped as a protractor wasn't needed. If you do use a plain bit of paper the lines should all be at a 60 degree angle to have 6 equal parts.
STEP THREE
Draw your snowflake pattern. The rule we stuck to when drawing ours was to copy exactly what we did on one of the 6 branches on each of the other five branches. They must be precise, they must be exactly the same on the other 5 branches...
Involving more maths...
This is where you can talk about reflection. We used a mirror and placed it in between the branches to demonstrate why it is a reflection. The pattern we had copied on to each branch should, if it is done correctly, look exactly the same as the reflection in the mirror.
For my seven year old we used the mirror as we went along. She didn't get it right but she had fun and it introduced her to why, with symmetry, it is important to get it right.
With my older girls we talked more about symmetry; we talked about how when we place the mirror in certain places on our snowflake sometimes the mirror reflected the same drawing we had made on the paper...
It has reflection symmetry! The snow flake looked the same with the mirror as without it. At this point you have found the axis of symmetry: this is a line through a shape so that each side is a mirror image.
And sometimes it didn't...
Then I encouraged the girls to turn the paper and see how many rotations they could make where the shape still looked the same. This is called rotational symmetry. If a shape will only fit itself in one way, if you rotate it it will always look different, that means there is no rotational symmetry in it.
When the drawing of a snowflake has been conquered, you might like to follow this project on further and think more about reflections and rotations. You might also like to think about translations and turning your snowflakes into a tessellation.
You might like to predict what shape your snowflake will be before unfolding it. Can you get it right?
Can you make your pattern using Hama beads?





Great project! It's wonderful how artistic math can be, isn't it? My girls are cutting out paper snowflakes these days....
ReplyDeleteThank you Annie! We've been cutting out snowflakes too. Those six pointed ones can get a bit tricky ;) xx
DeleteI'm going to do this with my 9 and 11 year olds for maths tomorrow! Thanks so much for sharing.
ReplyDeleteHi Lucinda, Great to hear! x
DeleteLovely idea - great way of getting them to see the potential in isometric paper! Thank you for all your ideas.
ReplyDeleteThank you Angela xx
Delete